力の表し方と物体に働く力
物体に力を加えると、静止しているものを動かしたり、動いているものを静止させることができ、さらに物体を変形させたり、破壊させることができます。
力をF、物体の質量をm、加速度をαとすれば、
F = mα ・・・・・・・・・・①
すなわち、力は質量×加速度の積で表すことができます。これはニュートンの第2法則といいます。
式①の単位は力Fを[N;ニュートン]、質量mを[㎏]、加速度αを[m/sec2]でそれぞれ表します。
注:mは単位メールを表し、質量mは記号です。
重さと質量の関係
地球上にある物体は、地球の中心に向かう加速度(重力の加速度)を常に受けています。この重力の加速度をg(g=9.8m/sec2とする)とおけば、式①より66㎏の体重は、
F = 66×9.8[N]≒647[N] ・・・・・・・・・・②
となり、これは地球がある物体に647[N]の力を加えたことになります。
このように力を加えることを、荷重を加える、あるいは付加するといいます。我々が日常において、重さ・重力というのは式①のmで表している質量のことを指しており、材料の力学で荷重という場合は、重さに重力を掛け合わせたものです。
力のモーメント
ボルトやナット、ネジを締めたり、緩めたりする場合、物体をある軸を中心として回転させようとするとき、加える力が一定ならば回転中心から距離が長いほど楽に回転できます。
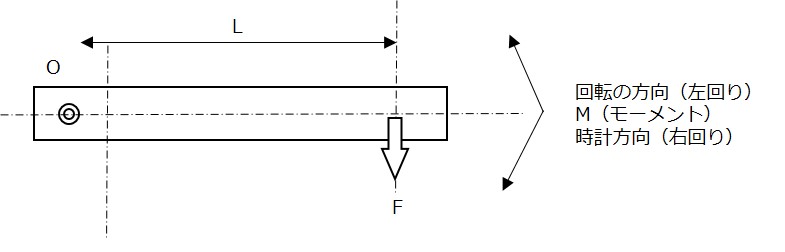
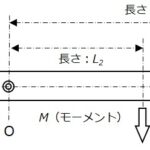
上の図に示すように、原点Oを中心として回転させる場合の回転作用の大きさは、加える力Fの大きさと原点Oから力Fの作用線までの距離Lとの積で表されます。これを点O周りの力のモーメント(moment)といいます。
力のモーメントをMとすれば M = FL ・・・・・・・・・・③となります。
ここで距離(長さ)Lをモーメントの腕といいます。また、力のモーメントは力F[N]と長さL[m]ので表すことにより、その単位は[N・m]で、材料の力学では[N・m(ニュートン・メートル)]、[kN・m(キロニュートン・メートル]、[kN・mm(キロニュートン・ミリメートル)]などを用います。力のモーメントは、右回り(時計回り)と左回り(反時計回り)とがあります。回転の方向によって正負の符号を付けます。通常、反時計回りを正とすることが多いので、ここでも反時計回り(左回り)を正とします。
モーメントの和(合力)
物体に多数の力F1、F2、 ・・・・・、Fnが作用している場合は、回転中心の点Oまわりの合力のモーメントは、点Oまわりの1つ1つの力のモーメントの和となります。力の作用している方向により、符号(正・負)が変わるので注意することが重要です。合力のモーメントをMで表せば
M = M1+M2+・・・・・+Mn = F111+F212+Fn1n
となります。
偶力
大きさが等しく、互いに平行な逆向き(作用する方向が反対方向)の一対の力を偶力といい、この偶力によって生じる力のモーメントを偶力のモーメントといいます。
ここでも回転方向によって正負の符号をつけ、力のモーメント同様に反時計回りを正とします。
偶力は物体を回転させる作用を持っており、その合力の値が0となります。
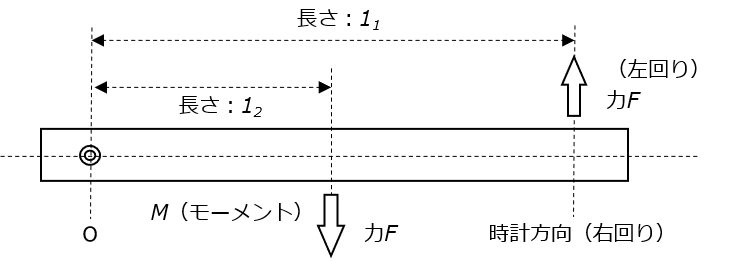
上図において、点Oまわりの偶力のモーメントをMとおけば
M = -F×11+F×12 = F(12-11)・・・・・・・・・・④
となります。ここで、12-11は回転直径となりますので、回転直径をdすれば、式④は
M = Fd ・・・・・・・・・・ ⑤
として表すことができます。式⑤には点Oからの距離(長さ)が入っていません。このことは点Oの位置に関わらず偶力のモーメントは一定の値Fdとなることを意味しています。偶力の作用線間の距離(回転直径)を偶力の腕といいます。
▼関連製品・他